Linear Discriminant Analysis - A Comprehensive Guide

LDA from Scratch

Dec 19, 2024

Intuition

The idea behind Linear Discriminant Analysis (LDA) is to dimensionally reduce the input feature matrix while preserving as much class-discriminatory information as possible. LDA tries to express the dependent variable as a linear combination of other features. Unlike ANOVA (Analysis of Variance) which analyzes differences among group means, LDA uses continuous independent features and a categorical output variable.

LDA attempts to distance the k classes as much as possible through a linear combination of its features by maximizing the between-class scatter while minimizing within-class scatter. LDA makes an assumption that for each of the $k$ classes, the class conditional densities p(x∣Y=k)=f_k(x) are multivariate Gaussian distributions.

Why does LDA make Gaussian assumptions?

One, it makes it mathematically easy to derive a closed-form solution for LDA. Two, through Maximum Likelihood Estimation (MLE), LDA's parameters can be estimated under Gaussian assumptions.

LDA assumes all classes have the same covariance matrix.

Simplification - Assuming equal covariance matrices for all k classes simplifies the LDA model. The assumption leads to linear decision boundaries between the classes aligning with LDA's linear combinations of features objective.

How is LDA different from PCA?

Principal Component Analysis (PCA) is different in its motives - it tries to maximize variance in the transformed features by finding directions/principal components that captures the highest overall variance. LDA works on maximizing class separability - it is class conscious and is a supervised method, whereas PCA is unsupervised. PCA is majorly used for dimensionality reduction whereas LDA is effective for classification tasks.

What does LDA do?

LDA tries to maximize the 'Between class distance' and minimize the 'intra class distance' for each class. Doing so will transform the original input space to a transformed lower dimensional space.

$f_k(\mathbf{x}) = \frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu}_k)^T\Sigma_k^{-1}(\mathbf{x} - \boldsymbol{\mu}_k)\right) $

Analyzing the decision boundary between the two classes where the discriminant functions are equal. The total between-class variance is calculated based on the below equation.

$ (\mathbf{m}_i - \mathbf{m})^2 = \mathbf{W}^T \mathbf{S}_{B_i} \mathbf{W} $

The below equation represents the discriminant's function for class k. The formula encapsulates the essence of LDA's classification mechanism, combining priors of the equation, covariance information, and distance of a data point from the class mean. By evaluating this function for each class and selecting the class with the highest score, LDA makes the classification decision. This below equation is after logarithm of f(x) since log is montonic and preserves the order of the original equation.

$ \delta_k(\mathbf{x}) = \log(\pi_k) - \frac{1}{2}\log(|\Sigma_k|) - \frac{1}{2}(\mathbf{x} - \boldsymbol{\mu}_k)^T\Sigma_k^{-1}(\mathbf{x} - \boldsymbol{\mu}_k) $

$ \delta_1(\mathbf{x}) = \delta_2(\mathbf{x}) $

$ \log(\pi_1) - \frac{1}{2}\log(|\Sigma|) - \frac{1}{2}(\mathbf{x} - \boldsymbol{\mu}_1)^T\Sigma^{-1}(\mathbf{x} - \boldsymbol{\mu}_1) = \log(\pi_2) - \frac{1}{2}\log(|\Sigma|) - \frac{1}{2}(\mathbf{x} - \boldsymbol{\mu}_2)^T\Sigma^{-1}(\mathbf{x} - \boldsymbol{\mu}_2) $

$ \log\left(\frac{\pi_1}{\pi_2}\right) - \frac{1}{2}(\boldsymbol{\mu}_1 + \boldsymbol{\mu}_2)^T\Sigma^{-1}(\boldsymbol{\mu}_1 - \boldsymbol{\mu}_2) + \mathbf{x}^T\Sigma^{-1}(\boldsymbol{\mu}_1 - \boldsymbol{\mu}_2) = 0$

This result is linear in $x$ and discriminates class 1 from class 2. x^Tx cancels out with the equal covariance assumption making the discriminant linear.

Constructing the Lower Dimensional Space

After calculating between-class variance, S_B and within-class variance, S_W, the lower dimensional matrix post transformation, W can be calculated based on Fisher's criterion.

$ \arg\max_\mathbf{W} \frac{\mathbf{W}^T \mathbf{S}_B \mathbf{W}}{\mathbf{W}^T \mathbf{S}_W \mathbf{W}} $

$ \mathbf{S}_W\mathbf{W} = \lambda\mathbf{S}_B\mathbf{W} $

$ (\mathbf{S}_W^{-1}\mathbf{S}_B - \lambda\mathbf{I})\mathbf{W} = \mathbf{0} $

$ \mathbf{W} = \mathbf{S}_W^{-1}\mathbf{S}_B $

Solution to the problem can be calculated from the eigenvalues and eigenvectors of the transformed matrix W. The eigenvectors show the directions of the transformed space and the eigenvalues shows the scaling factor - the discriminative power of the corresponding eigenvectors. Larger the eigenvalue, the more variance it accounts for in the direction of its corresponding eigenvector.

Building the LDA Model

Let's build an LDA classification model for binary classification.

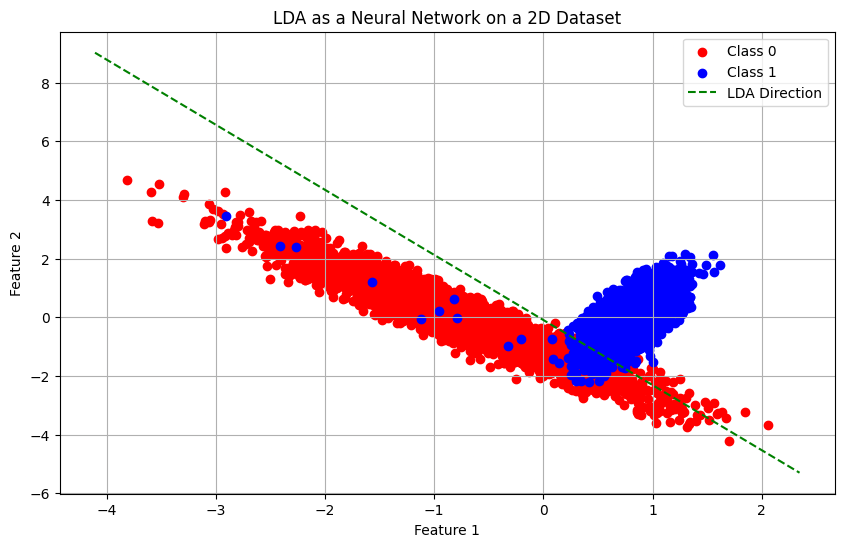
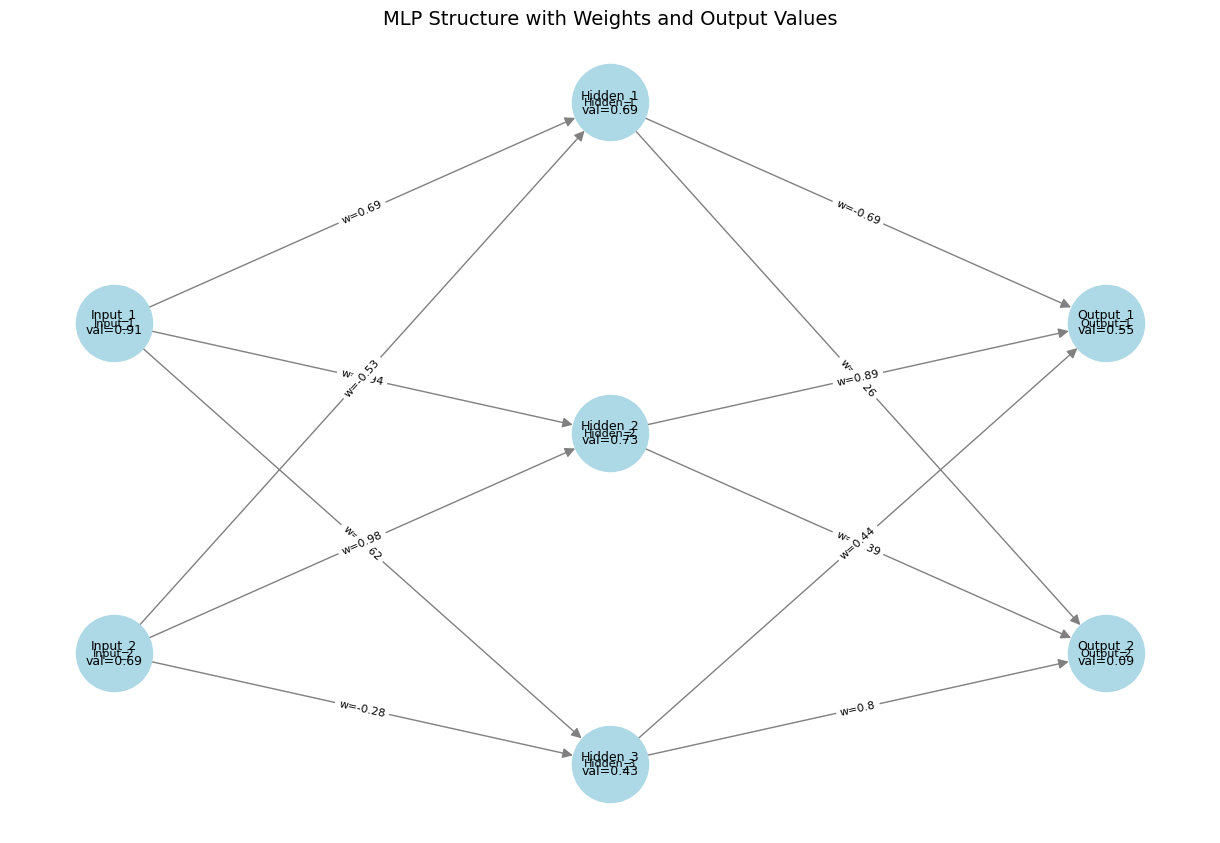
Formulating LDA as a Neural Network

The LDA classification model can be reformulated as a neural network with a single hidden layer. The input layer corresponds to the input data feature space and the output is a Softmax layer. The hidden layer is a single dense layer with a linear activation function. This layer performs the linear transformation defined by LDA. Weights of this layer correspond to the LDA directions (eigenvectors of the transformed matrix). Output Softmax layer converts the linear projection into class probabilities.

Training objective: Minimize cross-entropy loss, which is the same as maximizing class separability. Unlike LDA which computes a closed-form solution, the neural network can be trained using gradient-based optimizers.

References

[1] Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer. Chapter 4.3 discusses LDA in detail.

[2] Tharwat, A., Gaber, T., Ibrahim, A., & Hassanien, A. E. (20xx). Linear discriminant analysis: A detailed tutorial. AI Communications, 00, 1-22. DOI: 10.3233/AIC-170729

Siddharth’s Substack

Discussion about this post